(Cross-posted from Kayak Yak Yak)
And some Novembers, that’s just the way it feels.
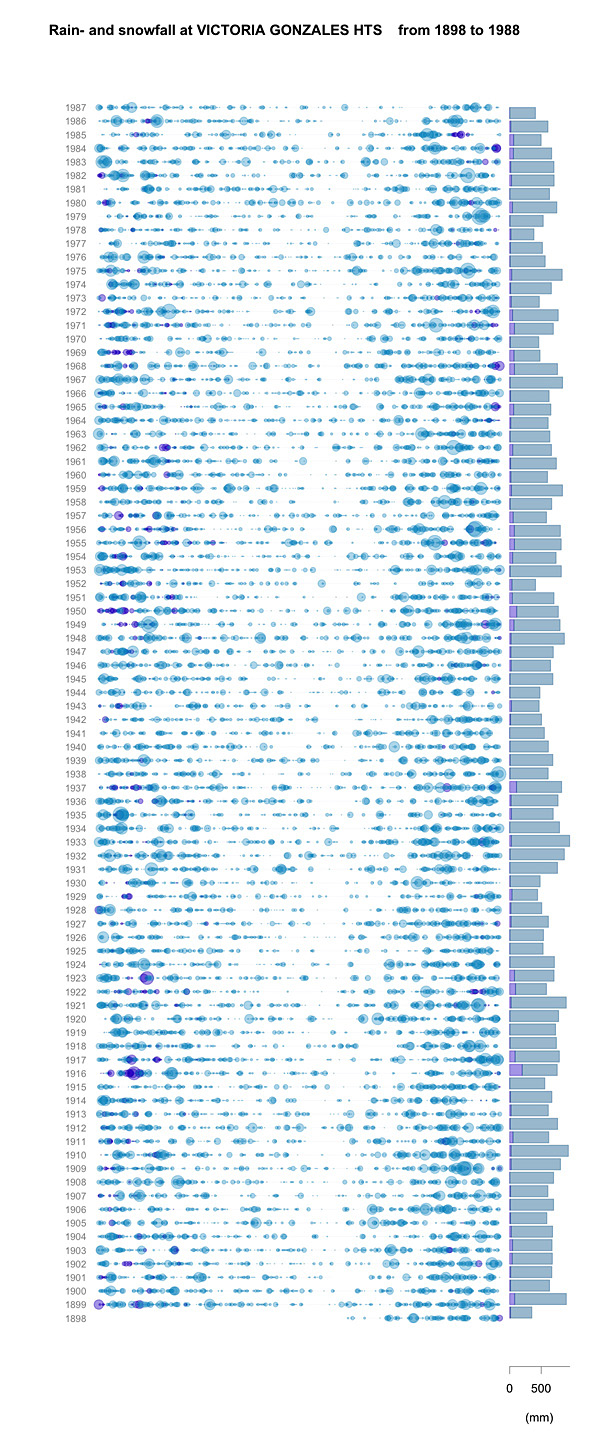
Inspired by this graphic, I have been playing around with the Canadian Daily Climate Data, available from Environment Canada National Climate Data and Information Archive. I’ll leave all the delightful geeky details of Python script and R code for another place and another time, but I wanted to show off my version of the plot, for the weather station at Gonzalez Heights (1898 to beginning of 1988). The area of the coloured circles are proportional to the rainfall, plotted per day along the horizontal and by year on the vertical (the San Francisco plot goes from mid-year to mid-year; mine currently uses the calendar year). On the right, the bars represent the total yearly precipitation. Rainfall is turquoise, snowfall is purple; snowfall is its liquid equivalent, not its snowy depth. During this period, the snowiest year was 1916 (199.4 mm by my calculation), with a one-day maximum of 53.3 mm (also in 1916). The rainiest year was 1933 (923.5 mm), although the maximum rainfall was 83.3 mm in 1979. Victoria International Airport has data from 1940 to 2004. None of these years (even 1996) was snowier, although the maximum snowfall, in 1996 (we know when that was!) was 64.5 mm. However the rainiest year was 1997, with 1159 mm, and the rainiest single day was in 2003, with 136 mm.